如果我们把训练模型的data比作炼丹的药材，那么模型就是炼丹炉，炼丹时候的火候就是优化器，正确的火候，能炼出牛逼的丹药，同样的，正确的优化器能练出泛化性能好的模型。

在我们整个深度学习的领域，优化器的基本算法都是基于梯度下降法，其他的方法例如牛顿法，利用二阶泰勒展开（比如xgboost就用到了这个优化方法）虽然从某种程度上来说，能够比梯度下降法得到更好更精确的结果，但是由于计算量等问题（二阶导是个成本比较高的问题），实际上，我们还是会用梯度下降法。

如果你不知道什么是梯度下降法，那么建议还是补下基础。

废话不多说，我们直接开始介绍具体的优化器，优化器具体可以被分为两类，第一类是非自适应优化器，第二类是自适应的优化器。前者在整个优化过程当中，学习率不变，或者按照时间变化，常见的例如SGD，SGDM。后者的学习率随着梯度自适应变换，并且尽可能去消去给定全局学习率的影响，这叫做自适应优化器，常见如Adagrad，RMSprop，Adam等。

原始的SGD每次只随机选择一个样本进行前向传播，然后反向计算梯度，原始SGD的速度非常快。但是缺点也是十分明显的，我们的损失函数可能会有很大的震荡，甚至难以收敛。

和SGD对应的是MBGD（Mini-batch gradient descent），或者有的时候，我们就把MBGD叫做SGD，MBGD每次利用一整个batch的样本，即利用n个样本进行计算。这样的好处是可以降低训练更新时候的方差，也使得收敛更加稳定，另外一方面，像pytorch等框架都对矩阵运算有各种优化，速度也不错。

mini-bactch也有一些缺点：如何选择合适的batch是一个问题，再者mini-batch依旧会陷入局部最小值，或者鞍点的位置。

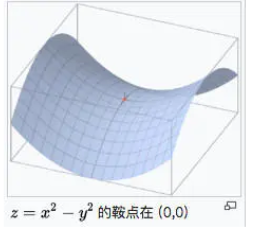
全称是SGD with momentum，于1986年提出，具体的公式为：

其中， 和 为超参数， 为模型的参数， 为损失函数，具体的参数的更新公式为：

一般而言，对于 我们设置初始化的值为0，那么就有：

依次类推，你会发现，当我们计算 且当 趋向于无穷的时候，会发现之前的梯度影响会越小。这样的方式，综合了之前的梯度的积累，会使得在梯度方向不变的方向上，下降速度变快，在梯 度方向上改变的地方，下降速度变慢（减少震荡）。

Adagrad随着迭代次数的增加，学习率会进行自动的衰减：

与SGD的区别在于，学习率除以前t-1次迭代的梯度的平方和，所以我们称之为自适应梯度下降。Adagrad也存在着问题，如果刚开始的梯度比较大，那么在训练的后期，学习率基本不会变化，成为了非自适应学习率。（由于累计平方梯度，导致学习率过快接近0）

RMSProp中修正了之前Adagrad导致的问题，主要是在累计平方梯度这个部分做文章：

推导一下：

随着迭代次数的增加， 中较前的部分的比例会越占越小，我们只关注近几次的平方梯度作为学习率变化的因子，这就解决了在Adagrad方法当中，由于累计平方梯度，最终导致学习率过快接近于0的状态。

Adam算法是将Momentum和RMSprop方法结合起来的方法，我们同时引用了两个参数 和 ，表达式为：

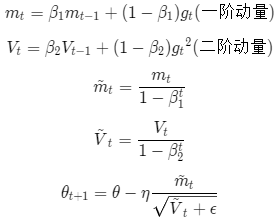
一方面考虑了梯度的衰减，一方面考虑了动量的累计（momentum）。此处的βt表示t次方，因为初始的梯度很小趋近于0，我们除以这个数可以进行修正。